Доказательство. Пусть точка М1(х1,
у1) – основание перпендикуляра, опущенного из точки М
на заданную прямую. Тогда расстояние между точками М и М1:
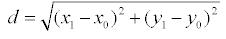 (1) (1)
Координаты
x1
и у1 могут быть найдены как решение системы
уравнений: 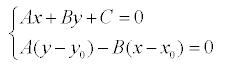
Второе
уравнение системы – это уравнение прямой, проходящей через
заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 +
By0 + C = 0,
то, решая,
получим: 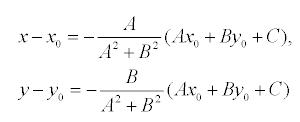
Подставляя
эти выражения в уравнение (1), находим: 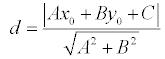
Теорема доказана.
|